I began the next section of discrete math. It covers predicates and quantifiers. These are the loops of the logic world, stretched blankets over exact universes. One quantification, the universal, implies a long conjunction: for every 
, apply AND to each of them. It takes one counterexample to show a universal quantification false.
I met the propositional function P(x), which encapsulates the subject and predicate of a statement. Specifying the domain lets us assign values to the variable. Since we’re in logic land, each such assignment evaluates to a truth value, True or False.
Multiple variables create instances of tuples. Databases also use the term tuple. Could the row of a database be an instance of a long function P(a, b, c, …, z)? The binding of one or more of those variables specifying uniqueness, and each row mapped to an array with one less dimension: tables as 2D, mappings as collapse to 1-dimensional, linear collections.
But I speak of fear. One example had math: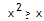 
. Rosen broke it down to 
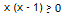. Then he goes to say it’s true if and only if 
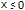or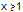 
. How did he get there? I became worried that my math journey would abruptly cease at section three, chapter one.
Wolfram Alpha gave hints, but ultimately I made a table:
Universe: real numbers x x*(x-1) x*(x-1)>=0 -2.0 6 T -1.5 3.75 T -1.0 2 T -0.5 2.25 T 0 0 T 0.5 -0.25 F 1.0 0 T 1.5 0.25 T 2.0 2 T
Somewhere between 0 and 1, the values we assign to the x variable do not result in a true inequality. Another way to say “x <= 0 or x >=1” is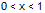 
. Can we believe that, though? What if there’s some number 0.000029482 that satisfies greater than or equal to zero? We can think through some assumptions:
x*(x-1) >= 0 A. if x = 0, x*(x-1) = 0 B. if x < 0, x * (x - 1) >= 0 (x - 1) <= 0 | divide by x (-), switches sign x <= 1 | add 1 to both sides x >= 1 | multiply by -1 on both sides (x is -)
The inequality is true when x <= 0.
x*(x-1) >= 0 A. if x = 1, x*(x-1) = 0 B. if x > 1, x * (x - 1) >= 0 (+) * (+) >= 0 | positive times positive is >= 0
The inequality is also true when x >= 1.
x*(x-1) >= 0 if 0 < x < 1, x * (x - 1) >= 0 (+) * (-) >= 0 ? | x (less than 1) minus 1 is negative (so, False)
When x is between 0 and 1, the inequality is false. Going back to the universal quantifier, for every x, P(x), with the domain of all real numbers, is false.
I generalized the process thus:
- Gather “data”: make a table. play with numbers. fiddle around. You are the compiler.
- Discover the “rules”: 0 < x < 1
- Check yourself: if x <= 0, if x >= 1, if 0 < x < 1
- Conclude: agree with the author or disagree; move on
In the Ever After 